Contents
Introduction
The Pythagoreans were a philosophical and religious community founded by Pythagoras of Samos in the 6th century BCE. Their history spans several centuries, including a period of flourishing, internal crises, and a lasting influence on ancient thought. Let’s examine their story in detail, structured by key stages.
1. The Foundation of the School and the Figure of Pythagoras
Pythagoras (c. 570–490 BCE) was born on the island of Samos in the Aegean Sea. Very little reliable information exists about his life, since the earliest biographies (such as those by Iamblichus and Diogenes Laërtius) were written centuries later and are full of legends. According to tradition, Pythagoras traveled extensively, studying the wisdom of Egypt, Babylon, and possibly India. These travels shaped his eclectic approach, combining mathematics, philosophy, religion, and mysticism.
Around 530 BCE, Pythagoras moved to Croton, a Greek colony in Southern Italy (Magna Graecia). There, he founded his school—not just an educational institution, but a closed community with elements of a religious order.
The Pythagoreans lived by strict rules, including communal living, vegetarianism, periods of silence, and rituals of purification.
The school had two levels:
- Akousmatikoi (“Listeners”): They followed religious and ethical precepts but did not delve deeply into scientific study.
- Mathematikoi (“Scientists”): They pursued philosophy, mathematics, astronomy, and music.
2. Pythagorean Doctrine
The Pythagorean doctrine was a synthesis of mysticism and rationalism. Its main aspects:
- Numbers as the Foundation of Reality: Pythagoreans believed that numbers were the essence of all things. For example, 1 represented a point, 2—a line, 3—a plane, 4—a solid. They studied the properties of numbers (odd/even, prime, perfect) and their relation to the cosmos.
- Harmony of the Spheres: They believed that the movements of heavenly bodies produced a kind of musical harmony, inaudible to the human ear. This idea connected astronomy, mathematics, and music.
- Metempsychosis: The doctrine of the transmigration of souls. Pythagoreans believed that the soul is immortal and, after death, passes into another being. This justified their vegetarianism and prohibition against killing animals. The term likely entered Greek thought under Eastern (Indo-Iranian) influence.
- Ethical Rules: The Pythagoreans followed a strict code, including the famous ban on beans (the reasons are unclear, possibly mystical or medical), an oath of loyalty to the school, and asceticism.
3. Political Activity and Crisis
The Pythagoreans were active in the politics of Croton and other cities of Southern Italy. Their elitist and aristocratic approach led to the establishment of oligarchic regimes supported by the school. However, this sparked discontent among democratic factions.
At the end of the 6th century BCE (c. 510–500 BCE), there was an anti-Pythagorean uprising in Croton. According to one version, the cause was popular resentment at the school’s closed nature and political influence. The house where the Pythagoreans met was set on fire; many died. Pythagoras himself is believed to have fled to Metapontum, where he died (the exact circumstances of his death are unknown).
After this, the school split into several groups. Some Pythagoreans left Italy, spreading the doctrine in other parts of Greece.
4. Reductionist Dogmatism: Number as Frame and Taboo
The history of the Pythagoreans is a classic example of how radical reduction can turn into dogma. In the context of “Deconstruction of Reality,” we can see it like this:
The Pythagoreans elevated numbers to the absolute. In their system, everything was reduced to numerical relationships.
It’s important to note that for the Pythagoreans, “number” meant only natural and rational numbers—that is, whole numbers and fractions. Their worldview was built on the conviction that everything could be expressed through relationships between whole numbers.
Reduction to number became not just a research method, but a frame of worldview, defining what could be considered real. Anything that did not fit into numerical harmony was declared either non-existent or hostile—irrational (in the literal sense: not expressible by rational numbers).
The dogma of number thus acted as a semantic “stop sign”:
All that exists is number.
All that is not number is outside the field of reality—dangerous or sinful.
This manifested not only in science but in the school’s organization itself: strict rituals, silence, taboos, secrecy, and bans on revealing knowledge. Reduction quickly turned into reductionist dogmatism—from a flexible method into an untouchable truth guarded by the order.
The Discovery of Irrational Numbers and the School’s Schism
Paradoxically, the very success of reduction led to the inner crisis of Pythagoreanism. During mathematical research, the Pythagoreans discovered the existence of irrational numbers—those that cannot be expressed as a ratio of whole numbers (such as \(\sqrt{2}\)). It turned out that the diagonal of a square and its side are incommensurable—there’s no number to express their ratio in integers or fractions.
This discovery undermined the core dogma of the school:
If not everything is a number (in their sense of number as ratios of integers), then reality is broader than their worldview.
The reaction was typically dogmatic: according to legend, the discovery was kept secret, and the discoverer (Hippasus of Metapontum) was supposedly punished, perhaps even killed.
Thus, dogma protects itself not through dialogue, but through exile and concealment of the other.
From this point, the Pythagorean community began to fracture—some tried to preserve the purity of the dogma, while others (the so-called Neo-Pythagoreans) sought ways to expand the doctrine.
Form vs. Meaning: Closure and Disintegration
The real crisis of Pythagoreanism was not only mathematical but also social.
The school became a closed order, where form (rituals, oaths, secrecy) replaced the original meaning—the search for harmony in all things. The external threat (democratic movements in Croton) only exacerbated the internal stagnation.
Dogma became not a source of inquiry, but a rigid barrier—anything new or contradictory was seen as dangerous.
The school’s disintegration followed a classic pattern:
- Some disciples spread across Greece, but no longer as a unified community, rather as bearers of separate elements of the doctrine.
- The very institution of the Pythagoreans—with its rituals and secrecy—was destroyed or driven out of Croton.
- The influence remained, but as an intellectual tradition, not a rigid organization.
Proof of the Existence of Irrational Numbers
The most famous proof is the incommensurability of the diagonal and the side of a square:
If we take the side of a square as 1, then the diagonal, by the Pythagorean theorem, is \(\sqrt{2}\).
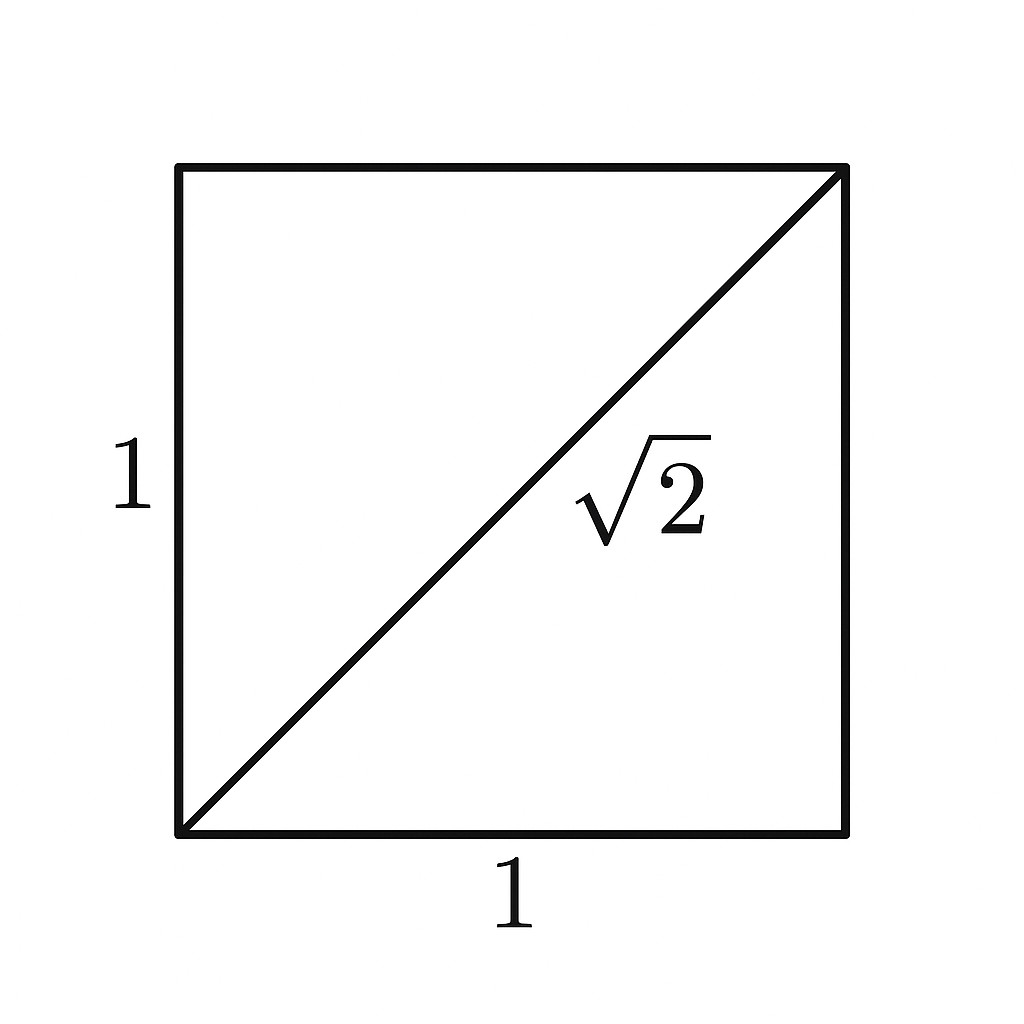
The Pythagoreans believed that any length could be expressed as the ratio of two whole numbers—that is, as a fraction \(m/n\). Let’s suppose \(\sqrt{2} = m/n\), where \(m\) and \(n\) are integers with no common divisors.
Squaring both sides gives:
\( (\sqrt{2})^2 = (m/n)^2 \)
\( 2 = m^2 / n^2 \)
\( 2n^2 = m^2 \)
This means \(m^2\) is even, so \(m\) must also be even (since the square of an odd number is always odd). Let \(m = 2k\), where \(k\) is an integer.
Plugging back:
\( 2n^2 = (2k)^2 = 4k^2 \)
\( 2n^2 = 4k^2 \)
\( n^2 = 2k^2 \)
So \(n^2\) is also even, hence \(n\) is even. But then both \(m\) and \(n\) are divisible by 2, contradicting our assumption that the fraction is in its lowest terms.
Conclusion: \(\sqrt{2}\) cannot be expressed as a fraction of whole numbers—it is an irrational number, directly contradicting the Pythagorean dogma.
This was the first step toward the realization that there are numbers beyond the “Pythagorean” numerical framework. Later, other irrationals like \(\pi\), \(3\sqrt{3}\), and so on were added.
A Subtle but Fundamental Lesson
It’s especially important to emphasize a subtle but fundamental point, often overlooked by those who believe in the full knowability of the universe. The discovery of irrational numbers proves that reality cannot be fully known. There exists an ontological limit — a boundary of knowledge that cannot be crossed by any amount of computation or even infinite time.
No matter how long you calculate, you will never reach the “end” of an irrational number: its decimal expansion is infinite, non-repeating, and never cycles. This is not a lack of knowledge, but a property of reality itself.
Therefore, to know everything “completely and for certain” is, by this very fact, fundamentally impossible. This undermines any faith that reality can be fully recreated or copied.
Any attempt at digital “cloning” of the world using computation faces an insurmountable barrier: computation always works with a finite number of digits, and can only ever approximate the original. Where reality contains infinite complexity (as with irrational numbers), any approximation will only ever be a likeness, not a true recreation. This is not a replica, but a simulacrum—necessarily incomplete and, in some sense, always false.
Irrational numbers are not just mathematical abstractions, but markers of a fundamental, insurmountable limit to human (and any algorithmic) knowledge.
Conclusion
The Pythagoreans were one of the most influential schools of antiquity, uniting philosophy, science, religion, and elements of politics. Their legacy is not only mathematical discoveries and rituals, but also the experience of building a closed community where the search for truth gradually gave way to strict dogma.
The school’s history took it from a period of rapid flourishing and real influence over the cities of Southern Italy to crisis, internal schism, and near-total disappearance. However, the Pythagorean ideas about the numerical nature of reality, harmony, and transmigration of souls had a huge impact on all later ancient cultures and European thought.
The symbolic turning point was the discovery of irrational numbers, which shattered their vision of the world as a perfect numerical harmony. This crisis revealed the limits of any closed system of knowledge and serves as a lesson: dogmatism inevitably leads to stagnation and collapse.
The experience of the Pythagoreans reminds us that no model of the world can capture all its complexity. Irrational numbers became not just a mathematical discovery, but a symbol of the infinite depth and mystery of being, which cannot be reduced to any formula or scheme.