Contents
1. From Philosophy to Mechanics
Before physics appeared in the modern sense, the word energy had a philosophical meaning. For Aristotle, energeia did not mean “a quantity of work” but actuality, opposed to potentiality (dynamis). Energy was the act of being — the realization of essence, the inner unfolding of a thing, the passage from possibility into reality. For the ancient mind, it signified presence — the living action of form.
Over time, this meaning changed. In the modern era, energy ceased to be the expression of an inner act and became a measurable quantity — an external expression of action, stripped of inner significance. The shift from “act of being” to “quantity of motion” was not merely linguistic; it marked a revolution in worldview. What once meant the presence of meaning became a metric of movement. Thus, energy was transformed from the expression of being’s meaning into a formula of action without meaning — not a step forward but a drift toward materialist reduction, where motion became more important than presence. Here was born the mechanistic metaphor of the world, where all existence could be described through movement, speed, and mass — and where meaning yielded to computation.
The idea of an inner act was replaced by the search for external laws of motion. When Galileo, in the seventeenth century, studied falling bodies, he discovered not only the regularity of velocity but also a mysterious constancy — a preserved “something” that passed between position and movement. Later, Newton laid the groundwork for understanding that “something”: motion could be measured by momentum, the product of mass and velocity, and forces were those things that changed momentum.
Yet the question remained: What exactly is conserved in motion? When a body stops, where does its “action” go? Philosophers and scientists of the eighteenth century sensed that behind changing velocities lay not just force but an inner reserve capable of transforming from one form into another. Thus arose the idea of energy — not as an instantaneous impulse but as a cumulative measure of action that could pass between forms without ever disappearing.

2. The Birth of Kinetic Energy
In the seventeenth and eighteenth centuries, physicists did not yet distinguish clearly between energy, force, and momentum. There was only an intuitive sense that motion contained something more than displacement — a capacity to perform work. Leibniz expressed this through the notion of vis viva, “living force.” He argued that the true measure of motion was not \(mv\), as Newtonians claimed, but \(mv^2\).
The idea was controversial at first, but it opened the way to seeing motion as a stored ability to act. A body moving twice as fast does not hit twice as hard — it hits four times as hard. Its action grows with the square of its velocity. This was not just speculation; experiments confirmed it.
Physicists realized that to accelerate a body to velocity \(v\) requires work proportional to \(v^2\), and this same work “returns” when the body stops. Thus was born the formula:
\(T = \frac{1}{2} m v^2.\)
To understand its logic, one must follow the reasoning of motion itself.
From Uniform Acceleration to the Path Equation
When motion is uniformly accelerated, velocity increases by equal amounts over equal times. Acceleration \(a\) is constant.
If initial velocity is \(v_0\), then after time \(t\):
\(v = v_0 + a t.\)
The distance \(s\) shows how far the body travels. At constant speed, \(s = v t\). But under acceleration, velocity increases; thus we take the average velocity over the interval:
\(v_\text{avg} = \frac{v_0 + v}{2}.\)
Half the time the body moves slower, half faster — this averaging yields the correct total path:
\(s = v_\text{avg} t = \frac{v_0 + v}{2} t.\)
Substitute \(v = v_0 + a t\):
\(s = v_0 t + \frac{1}{2} a t^2.\)
This shows the path as the sum of two parts: the distance covered by initial motion and the part gained through acceleration.
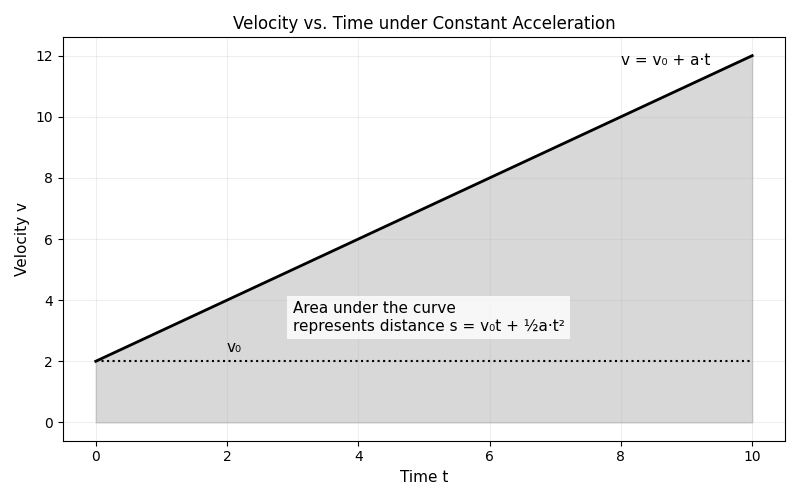
If the body starts from rest (\(v_0 = 0\)):
\(s = \frac{1}{2} a t^2.\)
From Work to Energy
Work is the product of force and distance:
\(A = F s.\)
According to Newton’s second law, \(F = ma\). Substituting \(s = \frac{1}{2} a t^2\):
\(A = (m a) \cdot \frac{1}{2} a t^2 = \frac{1}{2} m (a t)^2.\)
Since \(v = a t\), we get:
\(A = \frac{1}{2} m v^2.\)
The Meaning of the Formula
This is how the formula for kinetic energy is born. The coefficient \(\frac{1}{2}\) is not an arbitrary “correction,” but a numerical expression of average velocity, reflecting the fact that motion is a process of gradual accumulation. Kinetic energy is the total work done by a force while accelerating a body, averaged over the entire path. It preserves within itself the entire history of acceleration.
Looking deeper, the energy of motion is not merely a function of velocity but a manifestation of matter’s inner drive toward actualizing its own state. In every acceleration, in every transition from rest to motion, there is an imprint of that Aristotelian act — the passage from potentiality to actuality.
On a still deeper level, the formula \(\frac{1}{2}mv^2\) reveals that matter carries within itself an immaterial content. We can measure velocity — \(v\), the visible aspect, accessible to the eye and to instruments. But energy itself is proportional to \(v^2\) — to the square, which represents the inner, invisible dimension of the process. A body moves with velocity, yet exists in the state of energy. What truly acts cannot be observed directly — it is the immaterial yet effective foundation of motion.
Thus, the formula for kinetic energy expresses the dual nature of being: the visible velocity reflects the phenomenon, while the energy embodies the hidden essence — the inner meaning of action.
Energy is that which has no mass yet gives mass its meaning; that which occupies no space yet determines what occurs within space. It affirms that the immaterial is not only real — it is primary in relation to the motion of matter.
So it turns out that kinetic energy continues the ancient philosophical lineage: it expresses not only the mechanical but also the ontological property of matter — its innate striving to be.
By the nineteenth century, it became clear: motion is a form of storing work. The idea begun by Leibniz culminated in the principle of energy conservation. Every change in velocity, every interaction, is not the creation or loss of something new but the transformation between motion and position — between action and the expectation of action.
3. Potential Energy — The Energy of Position
The concept of potential energy appeared later than that of kinetic energy, and it marked a philosophical revolution: energy could exist not only in motion but in arrangement itself, even when nothing visible happens. A lifted stone or a stretched spring already contains the possibility of future action — a stored tension of the world, an anticipation of change.
From Force to Form
In the eighteenth century, from Robert Hooke to Joseph-Louis Lagrange, physicists sought to understand why systems return to equilibrium. Springs, pendulums, planets — all tended toward balance. Behind this lay the idea of a field — an invisible mediator through which bodies influence each other. Yet the realization that the field itself holds energy came only later.
For Newton, force acted instantaneously at a distance, without medium. Only in the nineteenth century did Michael Faraday and James Clerk Maxwell reveal a new picture: space itself is tense, structured, capable of storing and transmitting energy. From this insight grew the concept of potential energy as the energy of form — not of objects or motion, but of configuration itself.
Mathematical Formulation
When physicists realized that forces depending only on position could be expressed as the gradient of a function, it was a conceptual breakthrough:
\(\vec{F} = -\nabla V(q).\)
The gradient shows how and where the function \(V(q)\) changes most rapidly. If the potential is like a map of heights, the gradient points downhill, where energy decreases most quickly. The minus sign means force points toward equilibrium, toward lower energy.
One can say that the gradient is the direction of tension’s meaning — the path along which form seeks realization. Space ceases to be empty; it becomes a field of significance through which action flows.
The symbol ∇ (called nabla) represents an operator indicating how a function changes in space.
If \(V(x, y, z)\) assigns an energy value to every point, then its gradient is the vector of partial derivatives:
\(\nabla V = \left( \frac{\partial V}{\partial x}, \frac{\partial V}{\partial y}, \frac{\partial V}{\partial z} \right).\)
Each component shows how rapidly energy increases along that axis. Together they form the vector of greatest increase, and since force acts opposite to it, we write:
\(\vec{F} = -\nabla V.\)
Physics thus found a precise language for an ancient intuition: everything seeks home — the place of least tension.
The potential \(V\) became a universal tool for describing all conservative interactions, from mechanics to electrodynamics. The term itself comes from Latin potentia — “power,” “possibility.” It conveys the essence: energy resides not in bodies but in the relations between them.
Hence, force is the descent of energy toward ease, toward minimal tension, where form reaches rest.
Concrete Forms and Examples
For Earth’s gravity:
\(V_{\text{grav}} = mgh,\)
where \(m\) is mass, \(g\) gravitational acceleration, and \(h\) height. The higher the body, the more work was done — and the more energy stored in configuration.
More generally, for two masses \(M\) and \(m\) separated by \(r\):
\(V_{\text{grav}} = -\frac{G M m}{r}.\)
The minus sign indicates attraction: to separate them, one must invest energy against the field.
In elasticity (spring systems):
\(V_{\text{spr}} = \frac{1}{2} k x^2,\)
where \(k\) is stiffness and \(x\) elongation.
For electric charges:
\(V_{\text{el}} = \frac{1}{4\pi \varepsilon_0} \frac{qQ}{r},\)
with \(q\) and \(Q\) as charges and \(\varepsilon_0\) the electric constant; sign depends on attraction or repulsion.
In all cases, energy is no longer inside bodies — it is between them. The world is woven of relations, not things.
4. The Law of Conservation of Energy — The Rhythm of Transformation
By the nineteenth century, studies of heat, motion, electricity, and chemical reactions revealed a striking constancy: energy never disappears. It can shift forms — from motion to heat, electricity to light, tension to flow — but its total quantity remains the same. Independent thinkers — Julius Robert Mayer, James Joule, Hermann Helmholtz — made this clear. Mayer, noticing differences in sailors’ blood color across climates, inferred that heat is not a substance but a form of motion. Joule proved it experimentally by measuring the mechanical work required to heat water, linking action and heat. Helmholtz synthesized their insights into the principle of convertibility: energy is neither created nor destroyed, only transformed.
This became the heart of a new worldview. Everywhere in the universe transformations occur, yet the total balance endures. One may say the world lives by a law of conservation of meaning: action does not vanish but changes its mode of being. Where motion fades, form intensifies; where form collapses, flow ignites.
The law of energy conservation is thus not just physics — it is the law of the rhythm of existence: everything returns, everything transforms, everything persists in new form. And here science meets philosophy again: what Aristotle called energeia, the act of being, emerges as the invariant of physics. Energy is the unified essence of transformation, the bridge between motion and rest, flow and field, action and form.
5. Philosophical Afterword
At its deepest, kinetic energy is the energy of flow, potential energy the energy of field. Flow moves; field holds. Without flow, the world would freeze; without field, it would dissolve into chaos. Motion and form are complementary — the inhale and exhale of being.
This reveals a fundamental pattern of duality — a principle that permeates not only physics but the structure of reality itself. All existence oscillates between two poles: action and rest, change and stability, expansion and containment. Flow is the impulse of becoming, the surge of life; field is the memory of form, the structure that gives movement meaning. When they balance, the world endures; when one dominates, systems stagnate or disintegrate.
Flow is the unfolding of meaning in time; field is its retention in space. Their interplay weaves the fabric of reality, where every instant is a passage between possibility and act. Potential is the space of possibilities; kinetics, their realization. What exists as potential in one phase becomes action in another — and this rhythm is life itself.
Thus, the conservation of energy is not merely quantitative balance but a law of inner symmetry. What is lost in motion returns in form; what dissipates in action stabilizes in structure. It is not the exchange of matter but of meaning — the breathing of reality.
Energy is the rhythm of being. It does not belong to things but connects them in the pattern of becoming. At every moment the universe transforms tension into motion and motion into form, as though life itself were an eternal pulse between freedom and order.
The physics of energy is not just a branch of science — it is the language through which the universe tells the story of how meaning becomes action, and action returns to meaning.